公式速记
这部份是重要公式的汇总，证明在后面。
\[\begin{aligned} &A+BC=(A+B)(A+C)\\ &AB+\overline{A}C+BC=AB+\overline{A}C\\ &A+AB=A\\ &\overline{AB}=\overline{A}+\overline{B} \quad\quad \overline{A+B}=\overline{A}\cdot\overline{B}\\ &A\cdot\overline{AB}=A\overline{B} \quad\quad \overline{A}\cdot\overline{AB}=\overline{A} \end{aligned}\]基础运算
和运算
\[Y=A+B\]其运算规律为
\[\begin{aligned} 0+0=0\\ 0+1=1\\ 1+0=1\\ 1+1=1 \end{aligned}\]积运算
\[Y=A\cdot B\]其运算规律为
\[\begin{aligned} 0\cdot 0=0\\ 0\cdot 1=0\\ 1\cdot 0=0\\ 1\cdot 1=1 \end{aligned}\]异或(XOR) 运算
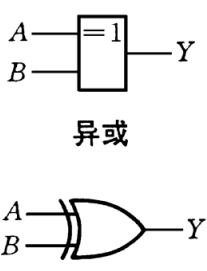\(Y=A \oplus B=A \overline{B}+\overline{A} B\)
其运算规律为
\[\begin{aligned} 0\oplus 0=0\\ 0\oplus 1=1\\ 1\oplus 0=1\\ 1\oplus 1=0 \end{aligned}\]当 $A$ 和 $B$ 不相同时，结果为 $1$；当 $A$ 和 $B$ 相同时，结果为 $0$；
也可以理解为『相加后模2』.
同或(XNOR) 运算
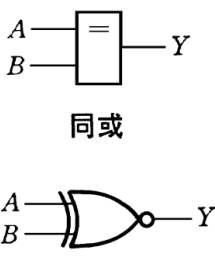\(Y=A \odot B=\bar{A} \overline{B}+ AB\)
其运算规律为
\[\begin{aligned} 0\odot 0=1\\ 0\odot 1=0\\ 1\odot 0=0\\ 1\odot 1=1 \end{aligned}\]相当于在『异或』运算后再去『非』；
也被称为『异或非』运算.
『异或』运算和『同或』运算有如下关系：
\[A \odot B=\overline{A \oplus B}\\ A \oplus B=\overline{A \odot B}\]基本公式
与 0 和 1 的运算
\[\begin{array}{c} 0 \cdot A=0 \\ 1+A=1 \\ \end{array} \quad \begin{array}{c} 1 \cdot A=A \\ 0+A=A \end{array}\]与自身运算
\[\begin{array}{c} A \cdot A=A \\ A \cdot \overline{A}=0 \\ A+A=A \\ A+\overline{A}=1 \\ \overline{\bar{A}}=A\\ \end{array}\]交换律、结合律和分配律
\[\begin{array}{c} A \cdot B=B \cdot A \\ A(B C)=(A B) C \\ A+B=B+A \\ A+(B+C)=(A+B)+C \\ A(B+C)=A B+A C \\ \end{array}\]若干常用公式及证明
\[\boxed{\overline{A B}=\overline{A}+\overline{B}}\] \[\boxed{\overline{A+B}=\overline{A} \cdot \overline{B}}\]这两个公式较为简单，写出真值表即可证明，略。
\[\boxed{A+B C=(A+B)(A+C)}\]
证明：
\[\begin{aligned} (A+B)(A+C)&=AA+AB+AC+BC\\ &=A(1+B+C)+BC\\ &=A+BC \end{aligned}\]\[\boxed{\mathrm{A}+\mathrm{AB}=\mathrm{A}}\]
证明如下
\[A+AB=A(1+B)=A\]\[\boxed{\mathrm{A}+\overline{\mathrm{A}} \mathrm{B}=\mathrm{A}+\mathrm{B}}\]
证明如下
利用 $A+B C=(A+B)(A+C)$ 展开等式左侧即可
\[A+\overline{A}B=(A+\overline{A})(A+B)=A+B\]\[\boxed{\mathrm{A}(\mathrm{A}+\mathrm{B})=\mathrm{A}}\]
证明
\[A(A+B)=A+AB=A(1+B)=A\]\[\boxed{\mathrm{A} \mathrm{B}+\overline{\mathrm{A}} \mathrm{C}+\mathrm{B} \mathrm{C}=\mathrm{AB}+\overline{\mathrm{A}} \mathrm{C} \\ \mathrm{A} \mathrm{B}+\overline{\mathrm{A}} \mathrm{C}+\mathrm{B} \mathrm{CD}=\mathrm{A} \mathrm{B}+\overline{\mathrm{A}} \mathrm{C}}\]
证明
观察法。以第一行的公式为例，
- 当 $A=0$ 时，左侧为 $B+BC=B$, 右侧为 $B$;
- 当 $A=1$ 时，左侧为 $C+BC=C$, 右侧为 $C$;
第二行公式同理.
\[\boxed{\mathrm{A\cdot\overline{AB}}=\mathrm{A} \overline{\mathrm{B}}} \quad \boxed{\overline{\mathrm{A}} \cdot\overline{\mathrm{AB}}=\overline{\mathrm{A}}}\]
证明
利用 $\overline{A B}=\overline{A}+\overline{B}$ 展开左侧，得
\[\mathrm{A\cdot\overline{AB}}=\mathrm{A\cdot(\overline{A} + \overline{B})}=0+ \mathrm{A} \overline{\mathrm{B}}\\ \overline{\mathrm{A}} \cdot\overline{\mathrm{AB}}=\mathrm{\overline{A}(\overline{A} + \overline{B})}=\overline{\mathrm{A}}+\overline{\mathrm{A}}\mathrm{B}=\overline{\mathrm{A}}\]练习题
并项法
利用公式 $AB+A\overline{B}=A$ 将两项合并为一项， 消去一个变量。
例题：
\[\begin{aligned} \mathbf{Y}_{1}&=\mathbf{A} \overline{\overline{\mathbf{B}} \mathbf{C} \mathbf{D}}+\mathbf{A} \overline{\mathbf{B}} \mathbf{C} \mathbf{D} \\ \mathbf{Y}_{2}&=\mathbf{A} \overline{\mathbf{B}}+\mathbf{A} \mathbf{C} \mathbf{D}+\overline{\mathbf{A}} \overline{\mathbf{B}}+\overline{\mathbf{A}} \mathbf{C} \mathbf{D} \end{aligned}\]解：
\[\mathbf{Y}_{1}=\mathbf{A} \overline{\overline{\mathbf{B}} \mathbf{C} \mathbf{D}}+\mathbf{A} \overline{\mathbf{B}} \mathbf{C} \mathbf{D}=\mathbf{A} \overline{\overline{(\mathbf{B}} \mathbf{C} \mathbf{D}}+\overline{\mathbf{B}} \mathbf{C} \mathbf{D})=\mathbf{A}\\ \mathbf{Y}_{2}=(\mathbf{A} \overline{\mathbf{B}}+\overline{\mathbf{A}} \overline{\mathbf{B}})+(\mathbf{A} \mathbf{C} \mathbf{D}+\overline{\mathbf{A}} \mathbf{C} \mathbf{D})=\overline{\mathbf{B}}+\mathbf{CD}\]吸收项法
例题：
\[\begin{aligned} \mathbf{Y}_{1} &=(\overline{\overline{\mathbf{A}}} \mathbf{B}+\mathbf{C}) \mathbf{A} \mathbf{B} \mathbf{D}+\mathbf{A} \mathbf{D}+\mathbf{A} \mathbf{D}\\ \mathbf{Y}_{\mathbf{2}}&=\mathbf{A} \mathbf{B}+\mathbf{A} \mathbf{B} \overline{\mathbf{C}}+\mathbf{A} \mathbf{B} \mathbf{D}+\mathbf{A} \mathbf{B}(\overline{\mathbf{C}}+\overline{\mathbf{D}})\\ \mathbf{Y}_{3}&=\mathbf{A}+\overline{\overline{\mathbf{A}} \cdot \overline{\mathbf{B} \mathbf{C}}} \mathbf{( \mathbf { A }}+\overline{\overline{\mathbf{B}} \overline{\mathbf{C}}+\mathbf{D}})+\mathbf{B} \mathbf{C}\\ \mathbf{Y}_{4}&=\mathbf{A} \mathbf{C}+\mathbf{A} \overline{\mathbf{B}}+\overline{\mathbf{B}+\mathbf{C}}\\ \mathbf{Y}_{5}&=\mathbf{A} \overline{\mathbf{B}} \mathbf{C} \overline{\mathbf{D}}+\overline{\mathbf{A} \overline{\mathbf{B}}} \mathbf{E}+\overline{\mathbf{A}} \mathbf{C} \overline{\mathbf{D}} \mathbf{E} \end{aligned}\]解：
\[\begin{aligned} \mathbf{Y}_{1} &=\mathbf{A} \mathbf{D}\\ \mathbf{Y}_{\mathbf{2}}&=\mathbf{A} \mathbf{B}\\ \mathbf{Y}_3 &=(\mathbf{A}+\mathbf{B}\mathbf{C})+(\mathbf{A}+\mathbf{B}\mathbf{C})(\mathbf{ \mathbf { A }}+\overline{\overline{\mathbf{B}} \overline{\mathbf{C}}+\mathbf{D}})\\ &=\mathbf{A}+\mathbf{B}\mathbf{C}\\ \mathbf{Y}_4 &=\mathbf{AC}+\mathbf{A}\overline{\mathbf{B}}+\overline{\mathbf{B}}\overline{\mathbf{C}}\\ &=\mathbf{AC}+\overline{\mathbf{B}}\overline{\mathbf{C}}\\ \mathbf{Y}_5 &=(\mathbf{A} \overline{\mathbf{B}})(\mathbf{C}\overline{\mathbf{D}})+(\overline{\mathbf{A} \overline{\mathbf{B}}}) \mathbf{E}+(\mathbf{C} \overline{\mathbf{D}})(\mathbf{E}) \overline{\mathbf{A}}\\ &=\mathbf{A} \overline{\mathbf{B}} \mathbf{C} \overline{\mathbf{D}}+\overline{\mathbf{A} \overline{\mathbf{B}}} \mathbf{E} \end{aligned}\]消因子法
利用 $\mathbf{A}+\overline{\mathbf{A}} \mathbf{B}=\mathbf{A}+\mathbf{B}$
\[\begin{aligned} \mathbf{Y}_{1} &=\overline{\mathbf{B}}+\mathbf{A} \mathbf{B} \mathbf{C}=\overline{\mathbf{B}}+\mathbf{A} \mathbf{C}\\ \mathbf{Y}_2 &=\mathbf{A} \overline{\mathbf{B}}+\mathbf{B}+\overline{\mathbf{A}} \mathbf{B}=\mathbf{A}+\mathbf{B}+\overline{\mathbf{A}} \mathbf{B}=\mathbf{A}+\mathbf{B}\\ \mathbf{Y}_{3} &=\mathbf{A C}+\overline{\mathbf{A}} \mathbf{D}+\overline{\mathbf{C}} \mathbf{D}=\mathbf{A} \mathbf{C}+\mathbf{(} \overline{\mathbf{A}}+\overline{\mathbf{C}}) \mathbf{D}\\ &=\mathbf{A C}+\mathbf{\overline{AC}D}=\mathbf{A C}+\mathbf{D} \end{aligned}\]题：化简表达式 $\mathrm{Y=AB+\overline{A}C+\overline{B}C}$
解： $\mathrm{Y=AB+(\overline{A}+\overline{B})C=AB+C}$
配项法
利用 $\mathbf{A+A=A}$
\[\begin{aligned} \mathbf{Y} &=\overline{\mathbf{A}} \mathbf{B} \overline{\mathbf{C}}+\overline{\mathbf{A}} \mathbf{B C}+\mathbf{A} \mathbf{B C}\\ &=(\overline{\mathbf{A}} \mathbf{B} \overline{\mathbf{C}}+\overline{\mathbf{A}} \mathbf{B C})+(\overline{\mathbf{A}} \mathbf{B C}+\mathbf{A} \mathbf{B C}) \\ &=\overline{\mathbf{A}} \mathbf{B}(\overline{\mathbf{C}}+\mathbf{C})+\mathbf{B C}(\mathbf{A}+\overline{\mathbf{A}})=\overline{\mathbf{A}} \mathbf{B}+\mathbf{B C} \end{aligned}\]利用 $\mathbf{A+\overline{A}=1}$
\[\begin{aligned} \mathbf{Y} &=\mathbf{A} \overline{\mathbf{B}}+\overline{\mathbf{A}} \mathbf{B}+\mathbf{B} \overline{\mathbf{C}}+\overline{\mathbf{B}} \mathbf{C} \\ &=\mathbf{A} \overline{\mathbf{B}}+\overline{\mathbf{A}} \mathbf{B}(\mathbf{C}+\overline{\mathbf{C}})+\mathbf{B} \overline{\mathbf{C}}+\mathbf{(} \mathbf{A}+\overline{\mathbf{A}}) \overline{\mathbf{B}} \mathbf{C} \\ &=\mathbf{A} \overline{\mathbf{B}}+\overline{\mathbf{A}} \mathbf{B} \mathbf{C}+\overline{\mathbf{A}} \mathbf{B} \overline{\mathbf{C}}+\underline{\mathbf{B} \overline{\mathbf{C}}}+\mathbf{A} \overline{\mathbf{B}} \mathbf{C}+\overline{\mathbf{A}} \overline{\mathbf{B}} \mathbf{C} \\ &=(\mathbf{ A} \overline{\mathbf{B}}+\mathbf{A} \overline{\mathbf{B}} \mathbf{C})+(\mathbf{B} \overline{\mathbf{C}}+\overline{\mathbf{A}} \mathbf{B} \overline{\mathbf{C}})+(\overline{\mathbf{A}} \mathbf{B} \mathbf{C}+\overline{\mathbf{A}} \overline{\mathbf{B}} \mathbf{C}) \\ &=\mathbf{A} \overline{\mathbf{B}}+\mathbf{B} \overline{\mathbf{C}}+\overline{\mathbf{A}} \mathbf{C} \end{aligned}\]综合法
\[\begin{aligned} \mathbf{Y} &=\mathbf{A} \mathbf{D}+\mathbf{A} \overline{\mathbf{D}}+\mathbf{A} \mathbf{B}+\overline{\mathbf{A}} \mathbf{C}+\mathbf{B} \mathbf{D}+\mathbf{A} \overline{\mathbf{B}} \mathbf{E} \mathbf{F}+\overline{\mathbf{B}} \mathbf{E} \mathbf{F}\\ &=\mathbf{A}+\mathbf{A} \mathbf{B}+\overline{\mathbf{A}} \mathbf{C}+\mathbf{B} \mathbf{D}+\mathbf{A} \overline{\mathbf{B}} \mathbf{E} \mathbf{F}+\overline{\mathbf{B}} \mathbf{E} \mathbf{F}(\text { 利用 } A+\bar{A}=1) \\ &=\mathbf{A}+\overline{\mathbf{A}} \mathbf{C}+\mathbf{B} \mathbf{D}+\overline{\mathbf{B}} \mathbf{E} \mathbf{F} \quad(\text { 利用 } A+A B=A) \\ &=\mathbf{A}+\mathbf{C}+\mathbf{B} \mathbf{D}+\overline{\mathbf{B}} \mathbf{E} \mathbf{F} \quad(\text { 利用 } A+\bar{A} B=A+B) \end{aligned}\]Author: Mike Lyou
Link: https://blog.mikelyou.com/2021/03/01/basic-boolean-algebra/
Liscense: This work is licensed under a CC BY-NC-SA International License.
